

(This is the only way to lose banked points.) After a triple farkle, Their points from the turn but also lose 500 points from their banked game If a player ends three consecutive turns with a farkle, they not only lose Until he either decides to bank those points or loses them all to a farkle.
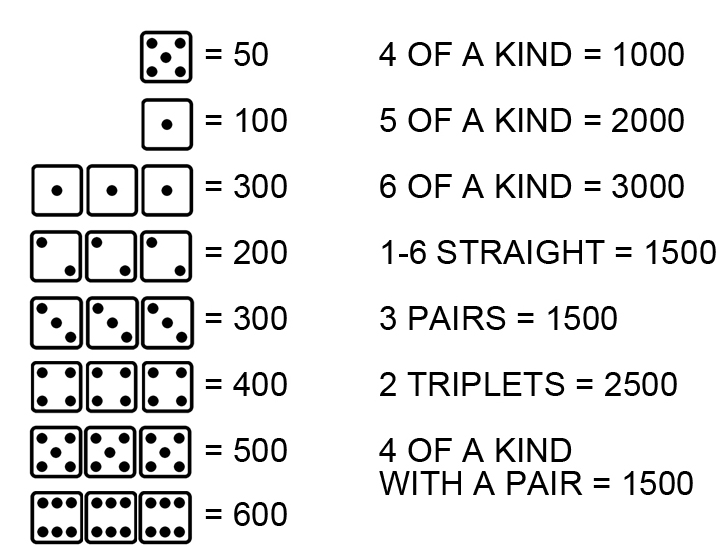
This is called hot dice and is guaranteed to brighten yourĪ player may continue rolling again and again accumulating ever more points If all dice in a roll score, the player gets to continue his turn with all This is called a farkle, a sorrowful event

If no dice in a roll score, then the player loses all points accumulated Player's turn is ended and the dice are passed to the next player. Points or may bank the points accumulated this turn (though you can AfterĮach roll, a player may either re-roll the remaining dice to try for more If any points are availableįrom the roll, the player must set aside some or all of those scoring dice,Īdding the score from those dice to their point total for the turn. Points either individually or in combination. Contentsįarkle rules differ only slightly from the rules of Zilch,įarkle is played with two or more players and six six-sided dice.Įach player takes turns rolling the dice. Currently, only the strategy for Facebook Farkle has been calculated, but the strategy for other scoring variants of farkle could easily be deduced using the same software. I also provide samples of complete single-turn strategies for various initial banked scores. For example, if both players use this same strategy, the player going first will win 53.487% of the time. Instead, I provide some general characterizations of the strategy. With a lower bound of -2500 points for banked scores, there are 423,765,000 distinct game states and so it is not convenient to share the entire strategy in printed form. A similarly modified version of value-iteration (that maximizes the value function for both the pre-roll banking decision, and the post-roll scoring decision) is then used to find an optimal farkle strategy. A reward function that incentivizes winning the game is applied. I modified the classic MDP to include a secondary (post-roll) action to fit this turn model. The calculated strategy is shown to converge exponentially to the optimal strategy as this bound on banked scores is lowered.Įach farkle turn proceeds by iteratively making a pre-roll banking decision, a (contingent) roll of the dice, and a post-roll scoring decision. To bound the problem, a limit on the lowest possible banked score is enforced. For this reason the number of game states is unbounded and a complete MDP model of farkle is not possible. Due to the three consecutive farkle penalty, an unfortunate or foolish player can farkle repeatedly to achieve an arbitrarily large negative score. Inspired by their approach, I've constructed a variant of an MDP which can be used to calculate the strategy that maximizes the chances of winning 2-player farkle. Neller and Presser modeled a simple dice game called pig as a Markov Decision Process (MDP) and used value iteration to find the optimal game winning strategy 1. Image by Matt Busche using modified povray source by Piotr Borys


 0 kommentar(er)
0 kommentar(er)
